الحاسوب الكمومي هو آلة تقوم بإجراء العمليات الحسابية اعتمادًا على مبادئ ميكانيك الكم. تتحكم هذه المبادئ في سلوك الجسيمات متناهية الصغر على المستوى الذري ودون الذري، وهي تختلف جذريًا عن القواعد التي تحكم الأجسام التقليدية في حياتنا اليومية. على سبيل المثال، وبخلاف الأجسام التقليدية، يمكن للجسيم الكمومي، في ظاهرة تُعرف بـ”التراكب الكمومي” (Quantum Superposition)، أن يوجد في مكانين مختلفتين في الوقت نفسه. قد يبدو ذلك للقارئ ضرباً من الخيال العلمي الذي يصعب تصوره، إلا أنها حقيقة علمية مثبتة بالتجربة، شأنها شأن باقي مبادئ نظرية الكم، والتي يمكن القول بثقة إنها واحدة من أنجح النظريات العلمية على الإطلاق.
منذ نشأتها قبل قرابة مئة عام، لم تأتِ أي تجربة علمية من بين الآلاف التي أُجريت بنتيجة واحدة تتعارض مع تنبؤات ميكانيك الكم. من بين هذه التنبؤات غير البديهية أيضًا ظاهرة التشابك الكمومي (Quantum Entanglement). وفقًا لهذه الظاهرة، يمكن لجسيمين كموميين أن يتفاعلا معًا بطريقة تُبقي على خواصهما متشابكة حتى عندما يتم فصلهما عن بعضهما بمسافات شاسعة تصل إلى مئات الآلاف من السنوات الضوئية. في هذه الحالة، يمكن للتفاعل مع جسيم على سطح الأرض أن يؤثر لحظيًا على جسيم آخر في مجرة بعيدة.
في الحوسبة الكمومية، تُمثَّل المعلومات باستخدام هذه الجسيمات الكمومية، ويتم استغلال قدرتها الفريدة على التراكب والتشابك لتنفيذ عمليات حسابية معقدة يصعب على الحواسيب التقليدية إنجازها في أي زمن معقول.
تمثيل المعلومات في الحواسيب الكمومية
في الحواسيب التقليدية، تُرمَّز المعلومات باستخدام النظام الثنائي كسلسلة من الأصفار والواحدات تُسمى البتات. يمثل البت (Bit) أصغر وحدة للمعلومات التقليدية، ويمكن أن يكون في إحدى حالتين: إما صفر أو واحد. جميع البيانات التي نستخدمها، من النصوص في رسائل البريد الإلكتروني إلى البيكسلات على شاشتك، هي في نهاية المطاف مجموعة من البتات التي تقوم الحواسيب بمعالجتها والتلاعب بها. على سبيل المثال، إذا أردت تخزين الرقم 9، فإن الحاسوب سيُمثلها كعدد ثنائي 1011.
بالمقابل، تستخدم الحواسيب الكمومية البت الكمومي، أو ما يُعرف اختصارًا بـ”كيوبت” (Qubit)، لتمثيل المعلومات. يختلف سلوك الكيوبتات عن البتات التقليدية بسبب خاصيتي التراكب والتشابك الكمومين:
- التراكب: على عكس البِت التقليدي الذي يمكن أن يكون إما 0 أو 1، يمكن للكيوبت أن يوجد في هاتين الحالتين في الوقت نفسه. يظل الكيوبت في هذه الحالة المتراكبة ما دام معزولًا عن البيئة الخارجية، إلا أنه عند محاولة قياس حالته (قراءة الكيوبت)، فإنها تنهار عشوائيًا إلى إحدى الحالتين: صفر أو واحد.
لتوضيح ذلك، يمكننا تخيل الكيوبت كعملة معدنية ذو وجهين (رأس وذيل) تم قذفها في الهواء. أثناء دورانها في الهواء، لاتمتلك العملة حالة محددة ويمكن القول أنها في حالة متراكبة من رأس وذيل في آن معاً. عندما تهبط العملة على سطح الأرض، عندها فقط يمكن تحديد حالتها بأحد الوجهين، إما رأس أو ذيل.
تسمح هذه القدرة للحواسيب الكمومية بأداء العديد من العمليات الحسابية في وقت واحد. على سبيل المثال، يمكن لنظام مكون من بتين تقليديين تمثيل واحدة فقط من أربع حالات ممكنة (00، 01، 10، أو 11)، ولكن نظام مكون من كيوبتين يمكن أن يمثل جميع الحالات الأربع في وقت واحد! ومع زيادة عدد الكيوبتات، يزيد عدد الحالات الممكنة بشكل أُسِي، مما يمنح الحواسيب الكمومية قدرة معالجة فريدة، و يسمح لها بحل بعض المشكلات أسرع بكثير من الحواسيب التقليدية. - التشابك: الخاصية الثانية التي تجعل الكيوبتات قوية للغاية هي التشابك. عندما يتشابك كيوبتان أو أكثر، فإن حالة أحد الكيوبتات ترتبط مباشرة بحالة الكيوبت الآخر، بغض النظر عن المسافة بينهما. وهذا يعني أن المعلومات حول كيوبت واحد يمكن استخدامها للتنبؤ بحالة كيوبت آخر، حتى وإن كانا متباعدين جدًا.
التشابك يشبه وجود زوج من العملات المعدنية ذات خواص سحرية. تخيل أنني أرسلت لك إحدى هاتين العملتين وأرسلت العملة الأخرى لصديقك الذي يسكن في المريخ. إذا رميت عملتك في الهواء، فستجد أن النتيجة عشوائية، إما رأس أو ذيل باحتمالات متساوية، شأنها شأن أي عملة معدنية عادية. سيحصل صديقك كذلك، عندما يرمي عملته، على رأس أو ذيل باحتمالات متساوية. حتى الآن، يبدو الأمر طبيعيًا جدًا. ولكن إذا التقيت بصديقك لاحقًا وقارنتما نتائج رمي العملتين، ستتفاجآن بأنه كلما حصلت أنت على “رأس”، حصل صديقك أيضًا على “رأس”، وكلما حصلت أنت على “ذيل”، حصل صديقك على “ذيل”! هذا الترابط بين حدثين عشوائيين مستقلين ومتباعدين مكانيا هو مايميز الكيوبتات المتشابكة.
في الحوسبة الكمومية، يسمح هذا التشابك بتبادل المعلومات بين الكيوبتات بشكل فوري وفعال للغاية. هذا “التأثير عن بعد” يمكّن الحواسيب الكمومية من أداء أنواع معينة من العمليات الحسابية بسرعة أكبر بكثير من الحواسيب التقليدية، التي تعالج كل بت بشكل منفرد.
تحتوى فقرة “نظرة أعمق“، في هذا القسم والأقسام التالية، على بعض التفاصيل الرياضية التي قد تثير اهتمام القرّاء ذوي الخلفية الأكاديمية. اذا كنت تفضل عدم الخوض في هذه التفاصيل، يمكنك ببساطة تخطي هذه الفقرة دون أن يؤثّر ذلك على فهمك لبقية المقال.
نظرة أعمق: حالة الكيوبتات وسعات الإحتمال
للمساعدة في تصور الفرق بين البت التقليدي والكيوبت، يمكن تشبيه حالة البت بسهم يشير إلى الأعلى إذا كان صفرًا أو إلى الأسفل إذا كان واحدًا. أما الكيوبت، فيُمكن اعتباره سهمًا يمكنه الإشارة إلى أي اتجاه. عادةً ما يُمثل ذلك هندسيًا باستخدام كرة تُعرف باسم كرة بلوخ (Bloch Sphere). على هذه الكرة، يمثل القطب الشمالي الحالة “صفر” ويمثل القطب الجنوبي الحالة “واحد”، بينما تمثل باقي النقاط على سطح الكرة حالات متراكبة. كلما اقتربت النقطة من القطب الشمالي، زاد احتمال قياس الكيوبت كصفر، وكلما اقتربت من القطب الجنوبي، زاد احتمال قياسه كواحد.
رياضيًا، يُستخدم رمز الكيت \(| \rangle \) لتمثيل حالة الكيوبت.على سبيل المثال، يستخدم الرمز \(|0\rangle\) لتمثيل حالة الصفر، والرمز \(|1\rangle\) لتمثيل حالة الواحد. بشكل عام، يمكن التعبير عن حالة الكيوبت كتركيب خطي لحالتي الصفر والواحد على النحو التالي: $$|\psi\rangle = \alpha |0\rangle + \beta |1\rangle$$ تدعى المعاملات \(\alpha, \beta\) سعات الاحتمال (Probability Amplitude) وهي التي تحدد بشكل غير مباشر احتمالات رصد القيمتين صفر أو واحد عند قياس حالة الكيوبت. على وجه التحديد، يُحسب احتمال رصد القيمة صفر كمربع القيمة المطلقة للمعامل الأول \(|\alpha|^2\)، بينما يُحسب احتمال رصد القيمة واحد كمربع القيمة المطلقة للمعامل الثاني \(|\beta|^2\). من المهم هنا التنبيه إلى الفرق بين سعات الاحتمال ومفهوم الاحتمالات التقليدية. فالاحتمالات التقليدية هي أعداد حقيقية تقع بين الصفر والواحد، بينما يمكن لسعة الاحتمال أن تكون عددًا سالبًا أو حتى عددًا عقديًا.
إذا أردنا تخزين حالة الكيوبت، فنحن بحاجة إلى تخزين الجزئين الحقيقي والتخيلي لكل من المعاملين \(\alpha, \beta\). أي أننا بحاجة إلى تخزين أربع قيم حقيقية. باستخدام الحواسيب التقليدية، يتطلب ذلك 128 بت من الذاكرة إذا افترضنا استخدام تمثيل الفاصلة العائمة وحيدة الدقة (Single Precision Float). من هنا يتضح أن قدرة الكيوبتات على تمثيل المعلومات تفوق بكثير قدرة البتات التقليدية، وتزداد هذه القدرة بشكل أُسِّي مع زيادة عدد الكيوبتات. على سبيل المثال، لتمثيل حالة كوبتين، نحتاج إلى أربعة معاملات تمثل سعات الاحتمال المرتبطة بكل من الحالات الأربع الممكنة لبتين تقليديين. يمكن كتابة هذه الحالة كالتالي: $$|\psi\rangle = \alpha |00\rangle + \beta |01\rangle + \gamma |10\rangle + \delta |11\rangle$$ بشكل عام، يتطلب تمثيل حالة \(n\) كيوبت تخزين \(2^n\) معامل ذو قيم عقدية. هذا يعني أن عدد البتات التقليدية اللازمة لتخزين حالة 250 كيوبت فقط يتجاوز عدد الذرات الموجودة في الكون بأسره!
هذا التضخم الأُسِّي في قدرة مجموعة من الكيوبتات على تمثيل المعلومات يرجع إلى ظاهرة التشابك الكمومي التي ذُكرت سابقًا، والتي تجعل حالة الكيوبت الواحد تعتمد على حالة بقية الكيوبتات في النظام. على عكس الفيزياء التقليدية، حيث يمكن توصيف الكل كمجموع لأجزائه، في الميكانيكا الكمومية لا يمكن وصف حالة مجموعة من الكيوبتات المتشابكة عن طريق توصيف كل كيوبت بشكل مستقل.
كمثال على ذلك، خذ هذه الحالة المتشابكة لكوبتين، والمعروفة باسم حالة بيل (Bell State): $$|\text{Bell State}\rangle = \frac{1}{\sqrt{2}}\left( |00\rangle + |11\rangle \right)$$ في هذه الحالة، هنالك احتمال 50% لرصد السلسلة 00 واحتمال 50% لرصد السلسلة 11. بالمقابل، فإن احتمال رصد السلسلتين 01 و 10 معدوم تماماً. مع أن احتمالية قياس كل كيوبت على حدة في الحالة صفر أو واحد هي 50%، فإنه بمجرد قياس أحد الكيوبتات وتحديد حالته، تتحدد حالة الكيوبت الآخر بشكل فوري لتكون متطابقة معه. الأمر الغريب هو أن هذا التأثير، حيث يؤدي قياس أحد الكيوبتات إلى تحديد حالة الآخر بشكل حتمي، يحدث بشكل لحظي، بغض النظر عن المسافة التي تفصل بين الكيوبتين.
معالجة المعلومات الكمومية
يمتلك هاتفك أو حاسوبك الذي تقرأ عليه هذه المقالة، معالج أو مايسمى بوحدة معالجة مركزية (CPU) تقوم بمعالجة البتّات لأداء مختلف المهام، بدءًا من العمليات الحسابية مثل الجمع والضرب، وصولًا إلى معالجة النصوص والصور. في النهاية، ينفذ المعالج جميع هذه المهام كعمليات منطقية على البتّات باستخدام بوابات منطقية مثل بوابات NOT وAND وOR.
بشكل مشابه، يمتلك الحاسوب الكمومي وحدة معالجة كمومية (QPU) تقوم بمعالجة الكيوبتات باستخدام بوابات كمومية (Quantum Gates). تؤدي البوابات الكمومية وظيفة مشابهة للبوابات المنطقية التقليدية، ولكن مع فارق رئيسي: فهي لا تقوم بتحويل الكيوبتات بين 0 و 1 فقط، بل تقوم بتغيير احتمالات وحالات الكيوبتات، مما يسمح لها بأداء عمليات أكثر تعقيدًا. بالعودة إلى تشبيه الكيوبت كعملة معدنية، يمكننا القول مجازًا أن البوابات الكمومية تتحكم في كيفية دوران العملة ووقت هبوطها.
كمثال على البوابات الكمومية، نذكر بوابة هادامارد التي تعد واحدة من أبسط البوابات. تأخذ هذه البوابة كيوبتًا في حالة محددة (مثل 0 أو 1) وتضعه في حالة تراكب. لذلك، إذا بدأ الكيوبت في حالة 0، فإن تطبيق بوابة هادامارد سيجعل الكيوبت في حالتي 0 و 1 في نفس الوقت (حتى يتم قياسه). من البوابات الكمومية المهمة أيضًا هي بوابة CNOT التي تعمل على كيوبتين معًا. تقوم هذه البوابة بتبديل حالة الكيوبت الثاني بناءً على حالة الكيوبت الأول. إذا كان الكيوبت الأول في حالة 1، فسيتم تبديل حالة الكيوبت الثاني من 0 إلى 1 وبالعكس. تُعد هذه البوابة أساسية لإنشاء حالة التشابك بين الكيوبتات.
نظرة أعمق: البوابات الكمومية
على الرغم من قدرة الحاسوب الكمومي على تمثيل كمٍّ هائل من المعلومات باستخدام عدد قليل نسبيًا من الكيوبتات مقارنة بالحاسوب التقليدي، إلا أن عملية قياس حالة هذه الكيوبتات تُنتج سلسلة عشوائية من الأصفار والواحدات، أي سلسلة من البتات التقليدية. تعتمد احتمالات رصد أي سلسلة معينة من هذه البتات على سعات الاحتمال التي تمثل حالة الكيوبتات عند القياس. لذلك، تتمثل مهمة الحاسوب الكمومي عند حل مشكلة معينة بالتلاعب بحالة الكيوبتات بحيث يصبح احتمال رصد السلسلة التي تمثل الجواب الصحيح مرتفعًا. يتم هذا التلاعب من خلال وحدات معالجة أساسية تُعرف باسم البوابات الكمومية. تعمل هذه البوابات على معالجة عدد محدود من الكيوبتات (غالبًا واحد أو اثنين) من خلال تعديل سعات الاحتمال المرتبطة بهذه الكيوبتات، وباستخدام مجموعة من هذه البوابات، يتم توجيه الحاسوب الكمومي ككل نحو الحالة التي تحمل الإجابة المطلوبة عند القياس.
يمكن مقارنة البوابات الكمومية مع البوابات المنطقية المستخدمة في الحواسيب التقليدية، مثل بوابات NOT, AND, OR. على سبيل المثال، تقوم بوابة النفي التقليدية (NOT) بعكس قيمة البت التقليدي: إذا كانت القيمة صفر تتحول إلى واحد، وإذا كانت واحد تتحول إلى صفر. بالمقابل، توجد بوابة نفي كمومية تؤدي وظيفة مشابهة، ولكنها تعمل على تبديل سعات الاحتمال المرتبطة بحالتي الصفر والواحد في الكيوبت: $$\alpha |0\rangle + \beta |1\rangle \xrightarrow{\text{ NOT }} \beta |0\rangle + \alpha |1\rangle$$
يمكن تصور هذا التغيير هندسيًا باستخدام كرة بلوخ (Bloch Sphere). عند تطبيق بوابة النفي الكمومية على حالة متراكبة للكيوبت، يتم تدوير السهم الممثل لهذه الحالة بمقدار 180 درجة حول المحور \(x\) على سطح الكرة.
أثر بوابة النفي الكمومية باستخدام كرة بلوخ [المصدر، معدّل]
بشكل أعم، فإن أي بوابة كمومية تُطبَّق على كيوبت واحد (وتُسمى بوابة كمومية أحادية أو Single-Qubit Gate) يمكن اعتبارها عملية تدوير للنقاط على سطح كرة بلوخ، حيث تختلف محاور وزوايا الدوران باختلاف نوع البوابة.
لاحظ أن أثر بوابة النفي الكمومية على حالتي \(|0\rangle\) و \(|1\rangle\) مكافئ تمامًا لأثر بوابة النفي التقليدية على البتات التقليدية. وبالتالي، فإن بوابة النفي الكمومية غير قادرة على خلق حالة متراكبة ابتداءً من حالتي \(|0\rangle\) و \(|1\rangle\). من بين أهم البوابات الكمومية الأحادية التي تُستخدم لخلق حالات متراكبة هي بوابة هادامارد (Hadamard Gate)، ويرمز لها بالحرف \(H\). تعمل هذه البوابة على نقل الكيوبت من حالة \(|0\rangle\) إلى حالة متراكبة بسعات احتمال متساوية كما يلي: $$|0\rangle \xrightarrow{\text{ H }} \frac{1}{\sqrt{2}} \left(|0\rangle + |1\rangle\right)$$
بشكل مشابه، تقوم بوابة هادامارد بتحويل الحالة \(|1\rangle\) إلى حالة متراكبة حيث تكون سعات الاحتمال متساوية في القيمة المطلقة ولكن بإشارتين مختلفتين: $$|1\rangle \xrightarrow{\text{ H }} \frac{1}{\sqrt{2}} \left(|0\rangle – |1\rangle\right)$$
تجدر الإشارة هنا إلى أن معرفة أثر البوابة الكمومية على حالتي \(|0\rangle\) و \(|1\rangle\) كافٍ تمامًا لتحديد أثرها على أي حالة متراكبة أخرى. السبب في ذلك هو أن أي حالة متراكبة يمكن تمثيلها كتركيب خطي من حالتي\(|0\rangle\) و \(|1\rangle\). وبالتالي، فإن أثر البوابة على أي حالة متراكبة يُمكن الحصول عليه من التركيب الخطي لأثرها على هاتين الحالتين الأساسيتين.
على سبيل المثال، يمكن استنتاج أثر بوابة هادمارد على أي حالة متراكبة كما يلي: $$\begin{align}
&\alpha |0\rangle + \beta |1\rangle \xrightarrow{\text{ H }} \\ &\frac{\alpha}{\sqrt{2}} \left(|0\rangle + |1\rangle\right) \; + \; \frac{\beta}{\sqrt{2}} \left(|0\rangle – |1\rangle\right) =\\ & \frac{\alpha+\beta}{\sqrt{2}} |0\rangle \; + \; \frac{\alpha-\beta}{\sqrt{2}} |1\rangle
\end{align}$$
نتيجة لذلك، يلعب مجال الجبر الخطي دورًا محوريًا في الحوسبة الكمومية، حيث يتم تمثيل الحالات الكمومية على أنها أشعة (Vectors)، بينما تُمثل البوابات الكمومية على أنها مصفوفات (Matrices) تؤثر على هذه الأشعة.
اقتصر حديثنا حتى الآن على البوابات الأحادية، والتي على الرغم من قدرتها على خلق حالات متراكبة لأي كيوبت بشكل منفرد، إلا أنها لا تُتيح التفاعل بين الكيوبتات المختلفة. وبالتالي، فهي غير قادرة بمفردها على خلق تشابك كمومي بين الكيوبتات. كما ذكرنا سابقًا، التشابك الكمومي عنصر أساسي في الحوسبة الكمومية (إلى جانب التراكب الكمومي)، فهو يُمكّن الكيوبتات من العمل كمجموعة مترابطة تُظهر خصائص لا يمكن تحقيقها باستخدام البتات التقليدية. هذه الخصائص هي التي تجعل الحوسبة الكمومية قادرة على تنفيذ الحسابات بفعالية غير مسبوقة.
لخلق التشابك الكمومي، نحن بحاجة إلى بوابات كمومية ثنائية (Two-Qubit Gates)، وهي بوابات تتحكم بحالة كيوبتين معًا. من بين أهم البوابات الثنائية وأكثرها استخدامًا هي بوابة النفي الخاضع للتحكم (Controlled-NOT أو CNOT). في الحاسوب التقليدي، تعمل بوابة CNOT على نفي البت الثاني (البت المستهدف) إذا كانت حالة البت الأول (البت المتحكم) 1، بينما تترك البت الثاني على حاله إذا كانت حالة البت الأول 0. من هذا التوصيف يمكن استنتاج أن أثر هذه البوابة في الحواسيب الكمومية على الحالة متراكبة لكيوبتين كالتالي: $$\alpha |00\rangle + \beta |01\rangle + \gamma |10\rangle + \delta |11\rangle \xrightarrow{\text{ CNOT }} \\ \alpha |00\rangle + \beta |01\rangle + \gamma |11\rangle + \delta |10\rangle$$ يمكن ملاحظة أن بوابة CNOT تبدل سعات الاحتمال للحالتين \(|10\rangle\) و\(|11\rangle\)، بينما تترك سعات احتمال الحالتين \(|00\rangle\) و\(|01\rangle\) دون تغيير.
على الرغم من بساطة بوابة CNOT، إلا أنها مع البوابات الأحادية، تشكل مجموعة كافية (Universal Gate Set) لتنفيذ أي خوارزمية كمومية يمكن تصورها. أي أن أي عملية حسابية كمومية يمكن تحقيقها باستخدام هذه المجموعة فقط. على سبيل المثال، يمكن تحضير حالة بيل، والتي تمثل حالة متشابكة بين كيوبتين، عن طريق البدء بالحالة \(|00\rangle\) وتطبيق بوابة هادامارد \(H\) على الكيوبت الأول، ثم تطبيق بوابة CNOT باستخدام الكيوبت الأول كمتَحَكم والثاني كهدف: $$ |00\rangle \xrightarrow{\text{ H (first qubit) }} \\ \frac{1}{\sqrt{2}} \left( |00\rangle + |10\rangle \right) \xrightarrow{\text{ CNOT }} \\ \frac{1}{\sqrt{2}} \left( |00\rangle + |11\rangle \right) $$
الخوارزميات الكمومية
الخوارزمية هي سلسلة من الخطوات والعمليات المحددة لحل مسألة معينة. يقوم حاسوبك الشخصي بتنفيذ هذه الخوارزميات على الدوام باستخدام مجموعة من البوابات المنطقية آنفة الذكر . كذلك يعمل الحاسوب الكمومي على تنفيذ الخوارزميات باستخدام مجموعة من البوابات الكمومية ضمن ما يُعرف بـ “الدارة الكمومية“(Quantum Circuit). يمكن القول أن الحاسوب الكمومي يتفوق على الحاسوب التقليدي في حل مسألة ما إذا عدد عمليات الخوارزمية الكمومية (وبالتالي زمن التنفيذ) أقل من عدد العمليات اللازمة في أي خوارزمية تقليدية لحل نفس المسألة.
نظرة أعمق: الدرات الكمومية
يتم تنفيذ أي حساب كمومي نريده باستخدام سلسلة من البوابات الكمومية والتي تُرتب بطريقة معينة في دارة كمومية. يتم عادة تمثيل هذه الدرات بمخطط يتم قرائته من اليسار إلى اليمين. في هذا المخطط، تُستخدم الخطوط الأفقية لتمثيل الكيوبتات، بينما يتم تمثيل البوابات الكمومية برموز تُوضع على هذه الخطوط وفقًا للكيوبتات التي تعمل عليها.
كمثال على ذلك، في مايلي مخطط الدارة الكمومية التي تقوم بتحضير حالة متشابكة لكيوبتين (حالة بيل) باستخدام بوابتي هادامارد وCNOT:
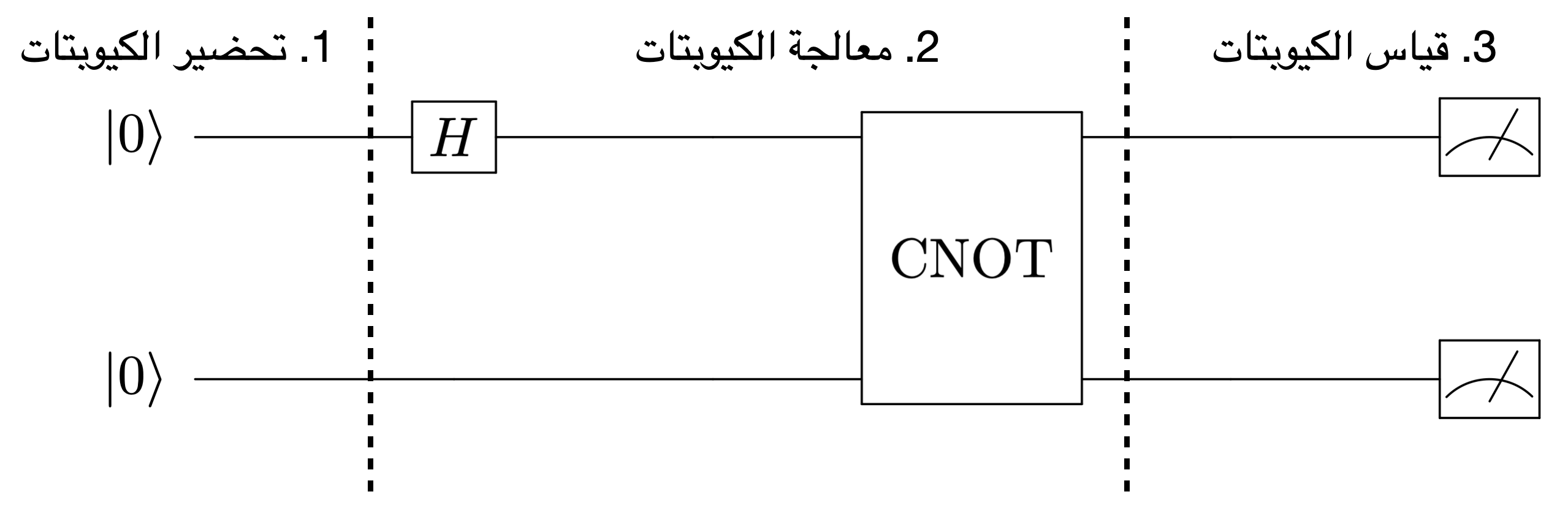
بشكل عام، يمكن تلخيص أي حساب كموكي أو خوارزمية كمومية بأربع خطوات أساسية:
- تحضير الكيوبتات في حالة ابتدائية غير متراكبة: يتم تهيئة جميع الكيوبتات في حالات محددة مسبقًا، غالبًا الحالة \(|00\dots0\rangle\) أو حالة أخرى ثابتة من الأصفار والواحدات، حسب متطلبات الخوارزمية.
- معالجة الكيوبتات باستخدام سلسلة من البوابات الكمومية: الهدف من هذه البوابات هو وضع الكيوبتات في الحالة الكمومية المرغوبة التي تمثل الحل المحتمل للمشكلة. تعتمد طبيعة هذه البوابات على نوع الخوارزمية والغرض منها.
- قياس حالة الكيوبتات: بعد المعالجة، يتم رصد حالة الكيوبتات، مما يؤدي إلى انهيار الحالة المتراكبة إلى سلسلة واحدة من الأصفار والواحدات. هذه السلسلة تكون موزعة عشوائيًا حسب سعات الاحتمال للحالة المتراكبة قبل القياس.
- تكرار العملية واستخلاص النتائج: يتم تكرار الخطوات السابقة عدة مرات للحصول على توزيع إحصائي للنتائج (سلاسل الأصفار والواحدات). تُستخدم هذه البيانات لتحديد الإجابة المطلوبة من خلال معالجتها باستخدام حاسوب تقليدي.
من أهم وأشهر الخوارزميات الكمومية هي خوارزمية شور (Shor’s Algorithm) التي تُستخدم لتحليل عدد صحيح إلى عوامله الأولية (Prime Factorization). تكمن أهمية هذه الخوارزمية في قدرتها على كسر معظم أنظمة التشفير الحديثة المستخدمة حاليًا على الإنترنت في وقت قياسي. معظم طرق التشفير الحديثة، مثل RSA، تعتمد على مفهوم صعوبة تحليل الأعداد الكبيرة إلى عواملها الأولية. في هذه الطرق، يتم اختيار عددين أوليين كبيرين يُمثلان المفتاح الخاص، وهو سر يُحتفظ به من قبل صاحب المعلومات المشفرة. بينما يتم حساب جداء هذين العددين ليكون المفتاح العام، وهو ما يُشارَك مع الآخرين. تعتمد أمان هذه الأنظمة على صعوبة استنتاج المفتاح الخاص (العوامل الأولية) من المفتاح العام (ناتج الجداء). باستخدام الحواسيب التقليدية، يُعد تحليل الأعداد الكبيرة إلى عواملها الأولية مشكلة معقدة زمنيًا، حيث يزداد الزمن اللازم للتحليل بشكل أسي مع زيادة طول العدد (Exponential Time Complexity). بالمقابل، فإن الزمن اللازم لتنفيذ خوارزمية شور على الحاسوب الكمومي يزداد بشكل متعدد الحدود (Polynomial Time Complexity). يعني ذلك عمليا أن كسر الشفرات الحالية على الحاسوب التقليدي يتطلب زمناً يتجاوز عمر الكون، بينما لن يحتاج الحاسوب الكمومي سوى بضع ساعات أو حتى دقائق لانجاز نفس المهمة.
من بين الخوارزميات الكمومية المهمة الأخرى هي خوارزمية غروفر (Grover’s Algorithm)، التي تُقدم تسريعًا كبيرًا لعمليات البحث في قواعد البيانات غير المرتبة. عند البحث في قائمة غير مرتبة تحتوي على \(N\) عنصر، يكون الهدف هو إيجاد عنصر يتمتع بخاصية معينة. باستخدام الحاسوب تقليدي، يتطلب العثور على العنصر المطلوب وسطيا فحص نصف العناصر، أي \(N/2\) خطوة. في أسوأ الحالات، قد يتطلب الأمر فحص جميع العناصر \(N\). بالمقابل، فإن استخدام خوارزمية غروفر يقلل عدد الخطوات اللازمة لإيجاد العنصر إلى حوالي\(\sqrt{N}\) فقط. يمثل ذلك تسريعًا تربيعيًا (Quadratic Speedup) مقارنة بالحواسيب التقليدية.
من التطبيقات المهمة أيضًا للحوسبة الكمومية هي محاكاة الأنظمة الفيزيائية على المستوى الكمومي للتنبؤ بخواص الجسيمات والمواد، مما يسمح بتسريع اكتشاف مواد جديدة ذات الخواص المرغوبة مثل الأدوية والنواقل الفائقة. تستطيع الحواسيب التقليدية محاكاة هذه الأنظمة، ولكن بشكل محدود جدًا، لأنه كما رأينا سابقًا، فإن تمثيل حالة الأنظمة الكمومية يتطلب قدرًا هائلًا من البتات التقليدية. من جهة أخرى، تُعد الحواسيب الكمومية منصة طبيعية لتمثيل هذه الأنظمة بشكل فعال ومحاكاة سلوكها بدقة أكبر وموارد أقل. في الواقع، فإن صعوبة محاكاة الأنظمة الكمومية على الحواسيب التقليدية هي التي دفعت العلماء إلى التفكير في أن لهذه الأنظمة قدرة خاصة على تمثيل كمية كبيرة من المعلومات، وبالتالي محاولة استغلال هذه القدرة، مما مهد الطريق لمجال الحوسبة الكمومية.
بالإضافة إلى ماسبق تَعِد الحوسبة الكمومية بثورة في الذكاء الإصطناعي وإيجاد الحلول المثلى في مجالات متعددة كالخدمات اللوجستية والنمذجة المالية وإدارة الموارد . هنا يجب التنويه إلى أنه، باستثناء بعض الخوارزميات مثل خوارزمية شور وخوارزمية غروفر ومحاكاة الجزيئات، لا توجد براهين رياضية على فائدة الحواسيب الكمومية في جميع هذه المجالات. لا يزال هناك الكثير من التكهنات، ويتطلب الأمر المزيد من البحث (الذي يجري حاليًا على قدم وساق) لاكتشاف خوارزميات كمومية يمكن البرهان رياضيًا على تفوقها. من المهم أن نؤكّد أن الحاسوب الكمومي ليس آلة سحرية قادرة على تسريع أي عملية حسابية مهما كانت. بل يجب اعتباره أداة مكملة للحاسوب التقليدي، حيث يمكنه حل بعض المسائل بشكل أكثر كفاءة. تتمثل أفضلية الحاسوب الكمومي على الحاسوب التقليدي في أنه يُقدم نمطًا جديدًا من البرمجة يسمح بتقليص عدد العمليات اللازمة لحل مسألة معينة وليس في تسريع كل عملية على حدة. هذه الأفضلية تختلف باختلاف المسألة المراد حلها ولا يجب أن نتوقع من الحاسوب الكمومي أن يوفر تسريعاً هائلاً في حل جميع المسائل. فمثلاً، يمكن البرهان رياضياً أنه لا توجد خوارزمية كمومية للبحث أسرع من خوارزمية غروفر. على الرغم من أن هذه الخوارزمية توفر تسارعاً تربيعياً مهماً جداً مقارنة بالخوارزميات التقليدية، إلا أنه يعتبر تسارعاً متواضعاً مقارنة بالتسارع الأسي الذي يعتقد البعض، خطأً، أن الحواسيب الكمومية سوف تكون قادرة على توفيره بدون قيود.
بناء الحاسوب الكمومي فيزيائيا
يتمحور كل النقاش السابق حول نموذج نظري للحوسبة الكمومية، والذي يفترض وجود جهاز فيزيائي قادر على تنفيذ البوابات الكمومية بشكل مثالي وبدون أخطاء. إلا أن واقع الأمر، أن هكذا جهاز مايزال قيد الدراسة والتطوير ،حيث تتسابق الدول والشركات في محاولة الوصول إلى حاسوب كمومي قابل للتوسع وبمعدل أخطاء منخفض.
من حيث المبدأ، يمكن بناء الكيوبت باستخدام أي جسيم أو نظام كمومي بحالتين مختلفين لتمثيل حالتي الصفر والواحد. يركز العلماء في أبحاثهم على أنظمة يمكنها البقاء في حالة متراكبة لأطول فترة زمنية ممكنة دون أن تتأثر بالبيئة الخارجية، وهو ما يُعرف بزمن إزالة الترابط (Decoherence Time). كذلك يبحث العلماء عن كيوبتات يسهل التحكم بالتفاعل في ما بينها من أجل تنفيذ البوابات الكمومية بوثوقية عالية أي بأقل قدر من الأخطاء. كذلك، يبحث العلماء عن كيوبتات يسهل التحكم في التفاعل بينها من أجل تنفيذ البوابات الكمومية بثقة عالية، أي بأقل قدر من الأخطاء. يوجد حالياً العديد من الطروحات المقترحة والنماذج الأولية لبناء الحواسيب الكمومية. تختلف هذه الطروحات في قابلية زيادة عدد الكيوبتات (Qubit Scalability)، وطول زمن إزالة الترابط، ووثوقية البوابات الكمومية (Gate Fidelity) وسرعتها، بالإضافة إلى القيود والتحديات الفيزيائية المرتبطة بتنفيذ هذه الطروحات.
من بين أكثر الطروحات الواعدة هي الكيوبتات فائقة الناقلية (Superconducting Qubits). تتكون هذه الكيوبتات من دوائر مصغرة مصنوعة من مواد فائقة الناقلية، والتي تسمح بمرور التيار الكهربائي بدون أي مقاومة. يؤدي انعدام المقاومة إلى امتلاك التيار لخواص كمومية محددة يمكن استغلالها في بناء كيوبتات ذات زمن إزالة ترابط طويل نسبياً يصل إلى رتبة المايكروثانية. يتم التحكم في هذه الكيوبتات باستخدام أمواج المايكروويف والتيارات الكهربائية، الأمر الذي يسمح بسرعة تنفيذ العمليات الكمومية مقارنة بالتقنيات الأخرى (سرعة البوابات من رتبة النانوثانية). من التحديات الرئيسية التي تواجه هذه التقنية هي الحاجة إلى تبريد شديد يقترب من درجة الصفر المطلق (-273.15 درجة مئوية). بالمقابل، تمتاز هذه الحواسيب بسهولة نسبية في التصنيع، حيث يمكن توظيف الآلات والتكنولوجيا المتقدمة المستخدمة حالياً في صناعة المعالجات التقليدية من أجل طباعة دوائر الحاسوب الكمومي فائق الناقلية.

تشكل الشوارد الحبيسة (Trapped Ions) إحدى التقنيات الواعدة الأخرى لبناء الحاسوب الكمومي. في هذه الحواسيب، تُستخدم الحالات الإلكترونية للشوارد لتمثيل حالتي الصفر والواحد وتراكباتهما. وبفضل شحنتها الكهربائية، يمكن حصر الشوارد وتعليقها في الفراغ باستخدام حقل كهرومغناطيسي، مما يسمح بعزلها عن البيئة الخارجية بشكل جيد، وبالتالي الحصول على كيوبتات بزمن إزالة ارتباط أطول مقارنة بالكيوبتات فائقة الناقلية (من رتبة بضع ثوان). يُستخدم الليزر للتحكم في حالة هذه الشوارد وتشابكها من أجل بناء البوابات الكمومية. تتميز هذه البوابات بوثوقية أعلى بشكل ملحوظ مقارنة ببوابات النواقل الفائقة، إلا أنها أبطأ بكثير، حيث تحتاج كل عملية إلى زمن من رتبة المايكروثانية. تمتاز الشوارد الحبيسة أيضاً بعدم حاجتها إلى التبريد الشديد كما هو الحال في الكيوبتات فائقة الناقلية، حيث يمكنها العمل في مجال بضع درجات فوق الصفر المطلق.
بالإضافة إلى الكيوبتات فائقة الناقلية والشوارد الحبيسة، توجد طروحات أخرى لا يتسع المجال هنا للخوض في تفاصيلها. من هذه التقنيات، على سبيل المثال لا الحصر: الحواسيب الكمومية البصرية الخطية (Linear Optics Quantum Computers)، التي تستخدم الفوتونات ككيوبتات، وحواسيب الذرات المعتدلة (Neutral Atoms)، التي تعتمد على ذرات ذات شحنة كهربائية معتدلة يتم تعليقها في الفراغ باستخدام أشعة ليزر عالية الدقة.
حاضر ومستقبل الحوسبة الكمومية
يطلق على الفترة الحالية من الحوسبة الكمومية فترة “نيسك” (NISQ)، وهو اختصار لمصطلح Noisy Intermediate-Scale Quantum، ويعني حواسيب كمومية ضوضائية ومتوسطة الحجم. يعود ذلك إلى أن جميع النماذج الأولية الحالية تعاني من مشاكل الضوضاء، أي أنها حتى الآن لا تستطيع القيام بعمليات كمومية دون أخطاء. بالإضافة إلى ذلك، فإنها تمتلك فقط عدداً متواضعاً من الكيوبتات لا يتجاوز بضع عشرات أو بضع مئات، حسب التقنية المستخدمة.
في عام 2019، أعلنت شركة غوغل (Google) عن معالج “سكمور” (Sycamore) ذو الـ 53 كيوبت، وبوثوقية تصل إلى 96.4%، والذي يعتمد على تقنية الكيوبتات فائقة الناقلية [المصدر]. كذلك أعلنت شركة غوجل مؤخرًا في كانون الأول/ديسمبر 2024 عن إصدار محدث من هذا المعالج الكمومي بعدد أكبر من الكيوبتات يصل إلى 105 كيوبت وبوثوقية أعلى، وأطلقت عليه اسم “ويلو” (Willow) [المصدر]. تمتلك شركة آي بي إم (IBM) أيضاً عدة حواسيب تعتمد على الكيوبتات فائقة الناقلية بأعداد مختلفة من الكيوبتات ودرجات متفاوتة من الوثوقية (بشكل عام، كلما ارتفع عدد الكيوبتات، انخفضت الوثوقية)، كان آخرها الجيل الثاني من معالج “هيرون” (Heron) ذو الـ 156 كيوبت، والذي أُعلن عنه في شهر تشرين الثاني/نوفمبر من عام 2024 [المصدر].
على صعيد آخر، توجد حواسيب الأيونات الحبيسة، التي توفر عدداً أقل من الكيوبتات لكنها تتمتع بدرجة أعلى من الوثوقية. على سبيل المثال، تمتلك شركة “آيون كيو” (IonQ) حاسوب “فورته” (Forte) بـ 36 كيوبت وبدرجة وثوقية تصل إلى 99.9%[المصدر]. كذلك، هناك حاسوب “H2-2” من شركة “كوانتينيوم” (Quantinuum)، الذي يمتلك 56 كيوبت بدرجة وثوقية تبلغ 99.87% [المصدر].
يتمثل التحدي الرئيسي في بناء الحواسيب الكمومية في هشاشة الحالات المتراكبة للكيوبتات وحساسيتها الشديدة للمؤثرات الخارجية. فكما ذكرنا سابقاً، يؤدي رصد الحالة المتراكبة إلى انتقال عشوائي للكيوبت إلى حالة الصفر أو الواحد. لا يحتاج هذا الرصد إلى وجود عنصر بشري كي يحدث، بل إن مجرد التفاعل مع البيئة الخارجية قد يؤدي إلى تعديل حالة الكيوبت بشكل غير مرغوب فيه. فمن ناحية، نريد عزل الكيوبتات قدر الإمكان حتى تحافظ على حالتها المتراكبة، ومن ناحية أخرى، نريد أن نكون قادرين على التفاعل معها لتنفيذ البوابات الكمومية ومعالجة المعلومات بالشكل المطلوب.
نتيجة لهذه التحديات، لا يزال بناء حاسوب كمومي كبير وخالٍ من الأخطاء أمراً بعيد المنال. ومع ذلك، يضخ المستثمرون والحكومات أموالاً طائلة في هذا المجال طمعاً في أن يكونوا أول من يضع يده على حاسوب كمومي قادر على القيام بما لا يمكن لأقوى الحواسيب التقليدية تحقيقه. على سبيل المثال، بلغ حجم التمويل الخاص بالشركات الناشئة في مجال التقنيات الكمومية في عام 2021 أكثر من 1.4 مليار دولار، وذلك دون احتساب التمويل الحكومي. حيث بلغ حجم التمويل الحكومي الكلي 1.9 مليار دولار في الولايات المتحدة الأمريكية و7.2 مليار دولار في الاتحاد الأوروبي، بينما تصدرت الصين قائمة الدول بتمويل إجمالي يصل إلى 15.3 مليار دولار [المصدر]. يعود ذلك إلى اعتبار العديد من حكومات الدول المتقدمة مسألة الحوسبة الكمومية قضية أمن قومي، نظراً لقدرتها المحتملة على فك العديد من الشفرات المستخدمة حالياً وإعطاء أفضلية غير مسبوقة في حل العديد من المسائل الحسابية المعقدة.
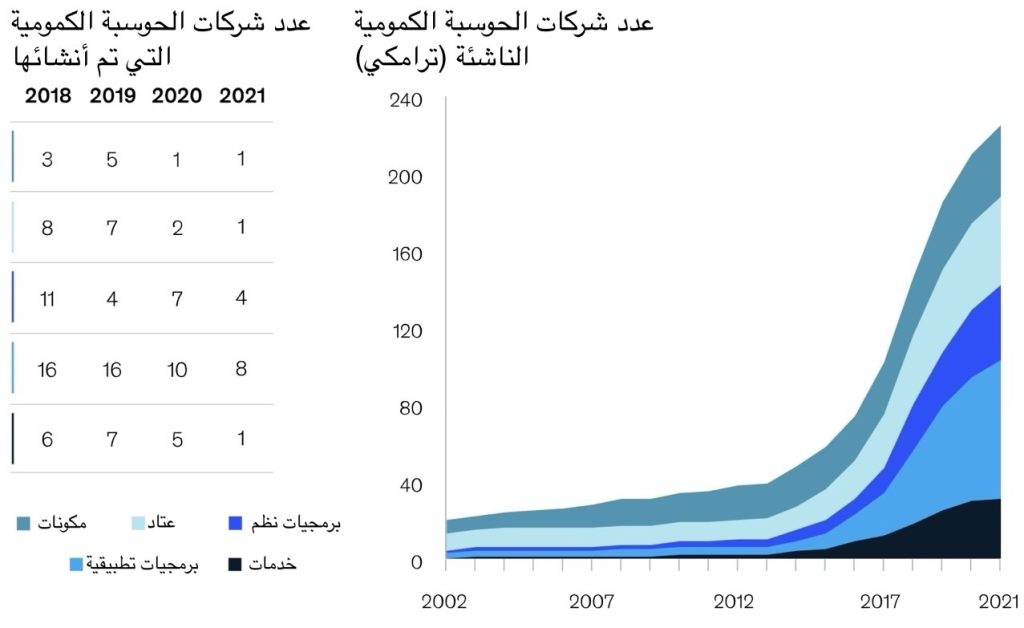
على الرغم من كل ما تعد به الحوسبة الكمومية والتقدم التقني الكبير الذي تحقق في العقد الماضي، لا يزال هناك من يشكك في إمكانية بناء حاسوب كمومي مفيد على المدى المنظور. إلا أن تاريخ التكنولوجيا مليء بأمثلة مشابهة، يصعب فيها التنبؤ بالمستقبل. على سبيل المثال، قبيل اختراع الأخوين رايت لأول طائرة تعمل بالمحرك، كان هناك العديد من المشككين في إمكانية تحقيق ذلك على أرض الواقع.
بالإضافة إلى ذلك، فإن الحواسيب التقليدية نفسها مرت بمراحل تقنية عديدة غير متوقعة. فأول حاسوب تقليدي، الذي اخترعه تشارلز باباج عام 1822، كان يعمل باستخدام بكرات ومسننات ميكانيكية. واستغرق الأمر أكثر من مئة عام للوصول إلى الحواسيب الإلكترونية التي تعمل بالصمامات المفرغة في ثلاثينيات القرن الماضي. كانت تلك الحواسيب ضخمة بحجم مبانٍ كاملة، واستغرق الأمر عشر سنوات أخرى لاختراع الترانزستور الذي مكننا من بناء حواسيب صغيرة الحجم وأكثر وثوقية.
إذا أسقطنا ذلك على الحوسبة الكمومية، فإن الحقيقة هي أنه لا يمكن لأحد أن يتنبأ بدقة بمستقبل الحواسيب الكمومية، وفيما إذا كنا على بعد بضع سنوات أم عشرات السنين من تحقيقها. هل يمكن مقارنة التكنولوجيا الكمومية الحالية بتقنية الترانزستور أم بالصمامات المفرغة؟ أم ربما ما زالت التقنيات الحالية بدائية إلى درجة تحتم مقارنتها بالبكرات والمسننات الميكانيكية؟
الوقت وحده كفيل بالإجابة على هذا السؤال!

